算数クイズ4 答えと解き方
答え
37
解き方
最多の場合の、切り分けられる部分を数えるので、
1つの交点で、3本以上の直線が交わることはない。
そうすると、新たに直線を1本引くごとに、
それまでに引かれた直線との交点が1つずつ増え、
分けられる部分の数は、(交点の数+1)つ分増える。
たとえば、
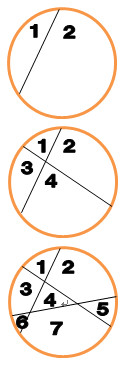
3本目の直線を引けば、
交点が2点増え、切り分けられる部分は3増える。
4本目の直線を引けば、
交点が3点増え、切り分けられる部分は4増える。
つまり、
X本目の直線を引けば、切り分けられる部分がXコ増える、
と言える。
したがって、
8本の直線の場合
1+2+3+4+5+6+7+8=36
ただし、1本目の直線を引く前から
円全体の1コの部分があるので
36+1=37となる。
 夢を実現させる心が育つ
進学塾チャレンジ1
本部教室 073-455-1727
夢を実現させる心が育つ
進学塾チャレンジ1
本部教室 073-455-1727



